When I say “Roll a Dice on a Quantum Computer”, technically there is no dice and it’s not entirely a click bait. I’m going to simulate and verify the probability of an 8 sided fair dice. Why would I want to waste resources to do such a simple task. Well, a simple answer. There is no point in whatever we do, if we can’t guarantee the correctness of the algorithm.
Why would you want to learn about Quantum Computing? Quantum Computing has open the door to a wide range of Quantum algorithms which are considered to be a threat to traditional encryption techniques. Most modern encryption techniques are based on the fact that there are no classic computers capable of computing large prime numbers. However, advanced Quantum computers will have the ability to break encryptions rendering current security standards to be worthless (eg:- ssl). So, things are about to get extremely exciting.
Quantum Computing versus Classical Computing
For now, let’s just stick with rolling a dice. 😉 Rigetti provides Quantum cloud computing services and is offering services under a beta release to the public. All the work in this post has been performed on Rigetti Quantum Computing services.
Let me briefly explain the difference between Quantum computing and classical computing. On a classical computer, information is stored in bits (discrete values which are either 1 or 0). In contrast, a quantum computer uses qbits to represent information and each qbit can either be 0 or 1. Due to the quantum properties, the measure would be probabilistic. A qbit can be in states |0} and |1}, but it can also be in a superposition of these states, c1|0} + c2|1}, where c1 and c2 are complex numbers. If we think of the state of a qbit as a vector, then superposition of states is a vector addition.
Simply, it means that if you have three qbits, at any time you measure, you will see either |000}, |001}, |010}, |011}, |100}, |101}, |110} or |111}. i.e. There are 2^n states where n is the number of qbits. In our case are 8 states and we are trying to simulate an 8 sided dice ;). If we can guarantee that each state is equally likely, we can guarantee the fairness of the dice and each state should have a probability of 1 / 8.
Development Environment
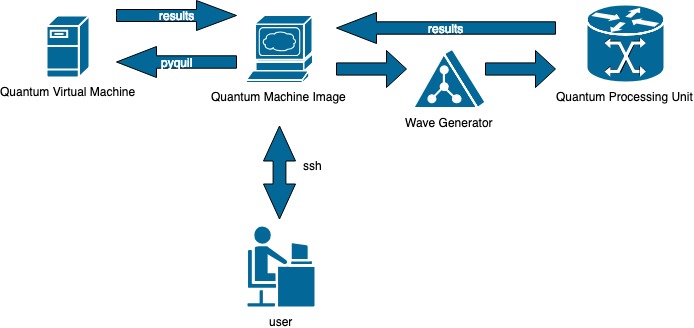
Let me briefly explain the architecture of the Quantum cloud. The user connects to a Quantum machine image (A linux server running CentOS). The framework is based on the pyquil python library. The python program is compiled to the Quil instruction set architecture and first simulated through the QVM (Quantum Virtual Machine). After the verification process, the user has to request for an allocation on the quantum machine to run the program on the actual QPU (Quantum Processing Unit), in the same way a user has to request for resources on a Super Computer.
Coding for a Quantum Computer
The following code has been obtained from “hello_qmi.py” program on the QMI of Rigetti Computing and has been modified to reflect the scenario. The copyrights of the code is with Rigetti and the modified version is published here with proper attribution. For information on the license, please refer examples given under https://github.com/rigetti/pyquil
Let me walk you through the code. There’s a lot of boiler plate code related to the job submission (which can and should be abstracted out by Rigetti in their later iterations).
def fair_dice(device_name: str = "9q-generic-qvm") -> None:
"""
Get acquainted with your quantum computer by asking it
to perform a simple fair-dice experiment. Involve 3
qubits in this experiment, and compute 100000 iterations.
:param device_name: The name of a quantum computer which
can be retrieved from
`pyquil.api.get_qc()`. To find a list
of all devices, you can use
`pyquil.api.list_devices()`.
"""
# Initialize your Quil program
program = Program()
device = query_device(device_name)
if device is not None:
# device_name refers to a real (QPU) device, so let's
# construct the program from the device's qubits.
readout = program.declare('ro', 'BIT', len(device['qubits']))
for qubit in device['qubits'].values():
program += RX(math.pi / 2, qubit)
for idx, qubit in enumerate(device['qubits'].values()):
program += MEASURE(qubit, readout[idx])
else:
# device_name refers to a non-real (QVM) device, so let's
# construct the program from arbitrary qubits, e.g. 0, 1,
# and 2
# Declare 3 bits of memory space for the readout results
# of all three qubits
readout = program.declare('ro', 'BIT', 3)
# For each qubit, apply a pulse to move the qubit's state
# halfway between the 0 state and the 1 state
program += RX(math.pi / 2, 0)
program += RX(math.pi / 2, 1)
program += RX(math.pi / 2, 2)
# Add measurement instructions to measure the qubits
# and record the result into the respective bit in
# the readout register
program += MEASURE(0, readout[0])
program += MEASURE(1, readout[1])
program += MEASURE(2, readout[2])
# This tells the program how many times to run the
# above sequence
program.wrap_in_numshots_loop(100000)
# Get the quantum computer we want to run our experiment on
qc = get_qc(device_name)
# Compile the program, specific to which quantum computer
# we are using
compiled_program = qc.compile(program)
# Run the program and get the array of results
results = qc.run(compiled_program)
# Print the results.
throw_polyhedral_die(6, results, 8)The first part of the function involves just defining the device and initializing the quantum program. The most important section is given below. This is where the real magic happens.
# For each qubit, apply a pulse to move the qubit's state
# halfway between the 0 state and the 1 state
program += RX(math.pi / 2, 0)
program += RX(math.pi / 2, 1)
program += RX(math.pi / 2, 2)In this code snippet, we apply a phase change to a wave function to move each qubit’s state halfway through. But why? By doing this we expect both 0 and 1 to be equally likely states for each qbit. Since these are three independent qbits the probability of any combination would be 1 / 2 * 1 / 2 * 1/ 2 = 1/ 8 which is equivalent to probability of an 8-sided fair dice.
Although the above code is performed on a QVM, we can also generate the code to be executed on the real QPU device in a similar manner.
readout = program.declare('ro', 'BIT', len(device['qubits']))
for qubit in device['qubits'].values():
program += RX(math.pi / 2, qubit)However, we still haven’t seen the method where the verification is calculated throw_polyhedral_die(6, results, 8). In this method, we convert each binary state (eg:- 001) to a binary value and count the number of occurrences. In the end we calculate the empirical probability using the frequencies observed.
def throw_polyhedral_die(num_sides, results, max_sides) -> None:
side_dict = dict()
for result in results:
number = 1 + int(''.join([str(x) for x in result]), 2)
if number in side_dict:
side_dict[number] += 1
else:
side_dict[number] = 1
print("Dice value, Probability")
for dice_value, obs in sorted(side_dict.items(), key=lambda k : k[0]):
print(f"{dice_value:6} {(obs / len(results)):8.4f}")Of course, we need the main method to provide the initiating point. The following code snippet does that.
if __name__ == '__main__':
import sys
if len(sys.argv) > 1:
fair_dice(device_name=sys.argv[1].strip())
else:
fair_dice()For completeness, the whole code looks like the following code snippet. Next, let’s look at the actual results.
import math
import numpy as np
from pyquil import Program, get_qc
from pyquil.api import QVM
from pyquil.gates import RX, MEASURE
from pyquil.api._devices import list_lattices
def query_device(device_name) -> dict:
"""
Try to query the device from QCS. Return the lattice dict
if it exists, or None otherwise.
"""
lattices = list_lattices()
if device_name in list(lattices.keys()):
return lattices[device_name]
return None
def throw_polyhedral_die(num_sides, results, max_sides) -> None:
side_dict = dict()
for result in results:
number = 1 + int(''.join([str(x) for x in result]), 2)
if number in side_dict:
side_dict[number] += 1
else:
side_dict[number] = 1
print("Dice value, Probability")
for dice_value, obs in sorted(side_dict.items(), key=lambda k : k[0]):
print(f"{dice_value:6} {(obs / len(results)):8.4f}")
def fair_dice(device_name: str = "9q-generic-qvm") -> None:
"""
Get acquainted with your quantum computer by asking it
to perform a simple fair-dice experiment. Involve 3
qubits in this experiment, and compute 100000 iterations.
:param device_name: The name of a quantum computer which
can be retrieved from
`pyquil.api.get_qc()`. To find a list
of all devices, you can use
`pyquil.api.list_devices()`.
"""
# Initialize your Quil program
program = Program()
device = query_device(device_name)
if device is not None:
# device_name refers to a real (QPU) device, so let's
# construct the program from the device's qubits.
readout = program.declare('ro', 'BIT', len(device['qubits']))
for qubit in device['qubits'].values():
program += RX(math.pi / 2, qubit)
for idx, qubit in enumerate(device['qubits'].values()):
program += MEASURE(qubit, readout[idx])
else:
# device_name refers to a non-real (QVM) device, so let's
# construct the program from arbitrary qubits, e.g. 0, 1,
# and 2
# Declare 3 bits of memory space for the readout results
# of all three qubits
readout = program.declare('ro', 'BIT', 3)
# For each qubit, apply a pulse to move the qubit's state
# halfway between the 0 state and the 1 state
program += RX(math.pi / 2, 0)
program += RX(math.pi / 2, 1)
program += RX(math.pi / 2, 2)
# Add measurement instructions to measure the qubits
# and record the result into the respective bit in
# the readout register
program += MEASURE(0, readout[0])
program += MEASURE(1, readout[1])
program += MEASURE(2, readout[2])
# This tells the program how many times to run the
# above sequence
program.wrap_in_numshots_loop(100000)
# Get the quantum computer we want to run our experiment on
qc = get_qc(device_name)
# Compile the program, specific to which quantum computer
# we are using
compiled_program = qc.compile(program)
# Run the program and get the array of results
results = qc.run(compiled_program)
# Print the results.
throw_polyhedral_die(6, results, 8)
if __name__ == '__main__':
import sys
if len(sys.argv) > 1:
fair_dice(device_name=sys.argv[1].strip())
else:
fair_dice()Results
First, let’s look at the execution results in the Quantum virtual machine environment.
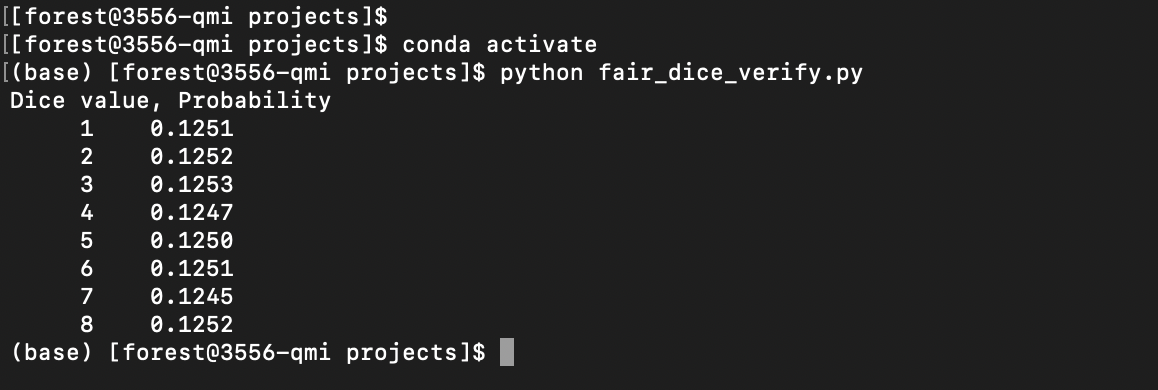
The theoretical value should be 1 / 8 (=0.125). All the values are approximately close to the theoretical value.
Next, let’s look at the execution results on the Quantum Processing Unit. The following experiment is performed on Aspen-3-3Q-B lattice which has 3 qbits.
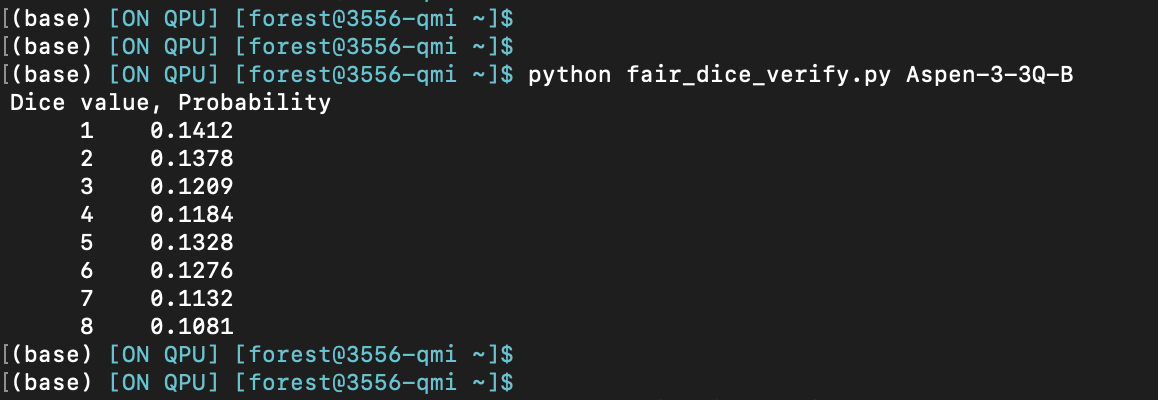
As you can see, we are not observing the expected value of 0.125. This could be due to the fact that there could be a bias when measuring the value of qbits (which map the quantum state to a classic state). In a perfect world, we would have observed exactly the same results.
Well, that’s it folks! We have simulated a dice on a Quantum computer.
Moving Forward
There are complicated quantum algorithms for search, factorization etc. I’m hoping to publish my research results as a series.
Regarding the disparity between the QVM and QPU results, it looks like the results are skewed toward basis states with more qubits in the ground state:
– |000> (all three qubits in ground state) has a probability of 0.1412
– |001>, |010>, and |100> (two of three qubits in the ground state) have probabilities 0.1378, 0.1209, and 0.1328
– |011>, |101>, and |110> (one of three qubits in the ground state) have probabilities 0.1184, 0.1276, and 0.1132
– |111> (none of the qubits in the ground state) has a probability of 0.1081
As the number of qubits in the ground state increases, the probability of rolling the corresponding die value increases. What this says to me is that either the gates were miscalibrated resulting in under-rotations that leave more population in the ground state than intended or the readout on these qubits is asymmetric, so “die values” corresponding to three-qubit states with more qubits in the ground state will have higher probabilities of being “rolled” than those with fewer qubits in the ground state.