Most of the implementations in the web for parallel merge sort do not consider how elements are divided between threads, if the total number of elements is not perfectly divisible by the number of threads. Also, the final merge (having joined all threads) should happen in a recursive manner.
But first, let’s go through a sketch of the algorithm. Any algorithm design requires understanding the underlying steps required to solve the problem. The following diagram shows the main components of the algorithm.
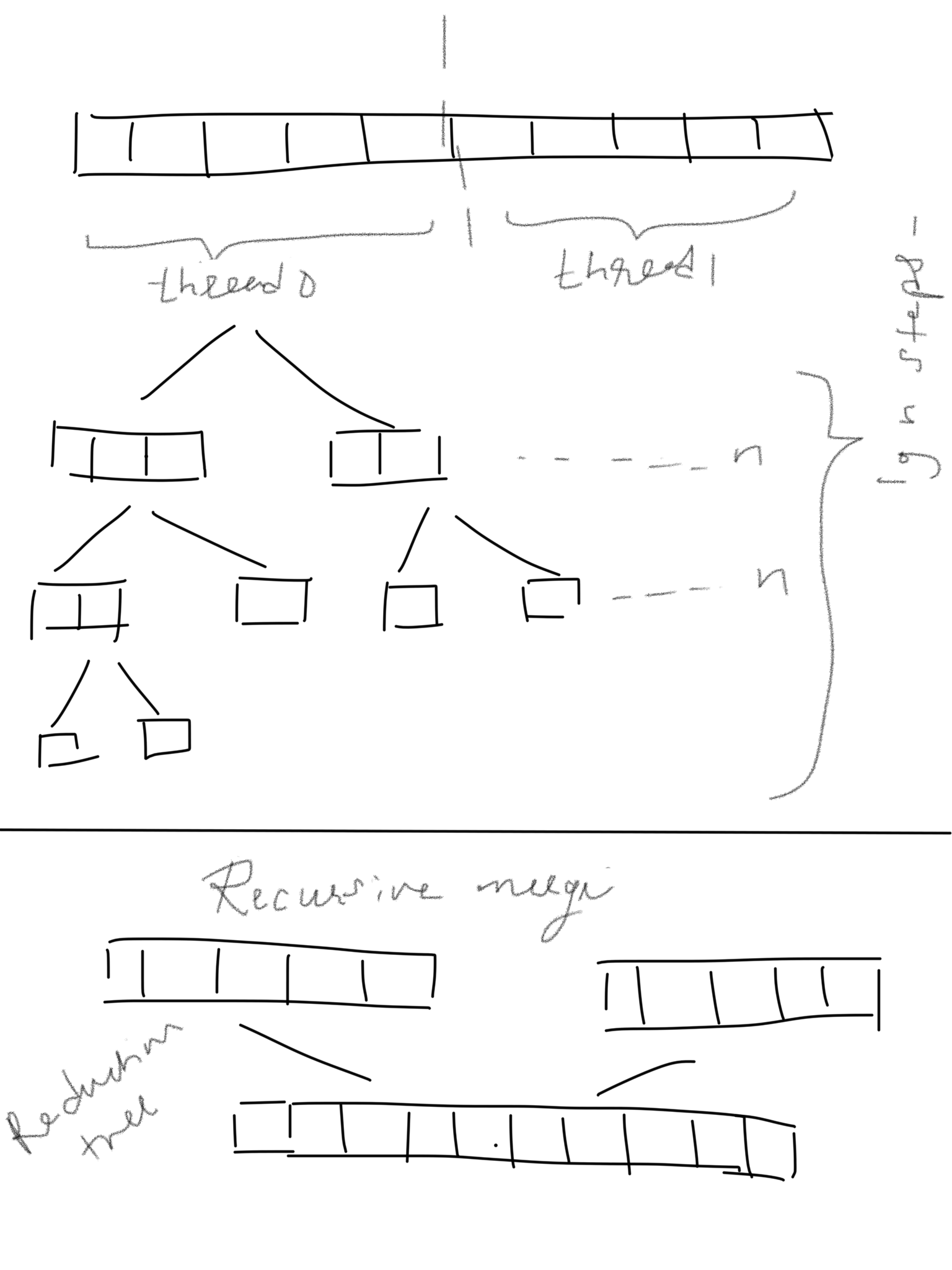
The top portion represents that the numbers are divided between threads (Namely thread 0 and thread 1). Afterwards, each thread would recursively perform merge sort on the portion of the array that it’s responsible for. At the end of this step we will have two portions of the array which are in the sorted order locally. Finally, we have to merge these portions to arrive at the globally sorted array. The second portion of the diagram depicts that we have to perform a recursive merge to get the globally sorted array.
Time Complexity
Merge sort has a time complexity of O(nlgn). At each step, we are performing the merge on n elements and there are lgn such steps resulting in a time complexity of O(n * lgn).
Rather than just sharing the code with you, let me walk you through the algorithm step by step.
void *thread_merge_sort(void* arg)
{
int thread_id = (long)arg;
int left = thread_id * (NUMBERS_PER_THREAD);
int right = (thread_id + 1) * (NUMBERS_PER_THREAD) - 1;
if (thread_id == NUM_THREADS - 1) {
right += OFFSET;
}
int middle = left + (right - left) / 2;
if (left < right) {
merge_sort(arr, left, right);
}
return NULL;
}The above function is fed in to the pthread call for the thread to work recursively. First it obtains the thread id and finds the left and right bounds in the array. Afterwards, it performs the usual merge sort. The difference between the serial version and the parallel version is that we have to figure out the bounds of the array to operate on, during the initial function call.
/* perform merge sort */
void merge_sort(int arr[], int left, int right) {
if (left < right) {
int middle = left + (right - left) / 2;
merge_sort(arr, left, middle);
merge_sort(arr, middle + 1, right);
merge(arr, left, middle, right)
}
}The above code is the usual merge sort that we are familiar with. I’ll also present the merge function where the actual merge happens.
/* merge function */
void merge(int arr[], int left, int middle, int right) {
int i = 0;
int j = 0;
int k = 0;
int left_length = middle - left + 1;
int right_length = right - middle;
int left_array[left_length];
int right_array[right_length];
/* copy values to left array */
for (int i = 0; i < left_length; i ++) {
left_array[i] = arr[left + i];
}
/* copy values to right array */
for (int j = 0; j < right_length; j ++) {
right_array[j] = arr[middle + 1 + j];
}
i = 0;
j = 0;
/** chose from right and left arrays and copy */
while (i < left_length && j < right_length) {
if (left_array[i] <= right_array[j]) {
arr[left + k] = left_array[i];
i ++;
} else {
arr[left + k] = right_array[j];
j ++;
}
k ++;
}
/* copy the remaining values to the array */
while (i < left_length) {
arr[left + k] = left_array[i];
k ++;
i ++;
}
while (j < right_length) {
arr[left + k] = right_array[j];
k ++;
j ++;
}
}
The most important section of the code is the final merge where we merge locally sorted array segments to form the globally sorted array. The below code segment shows how segments are merged pair wise recursively.
/* merge locally sorted sections */
void merge_sections_of_array(int arr[], int number, int aggregation) {
for(int i = 0; i < number; i = i + 2) {
int left = i * (NUMBERS_PER_THREAD * aggregation);
int right = ((i + 2) * NUMBERS_PER_THREAD * aggregation) - 1;
int middle = left + (NUMBERS_PER_THREAD * aggregation) - 1;
if (right >= LENGTH) {
right = LENGTH - 1;
}
merge(arr, left, middle, right);
}
if (number / 2 >= 1) {
merge_sections_of_array(arr, number / 2, aggregation * 2);
}
}And of course, no code is complete without a testing method. I’m checking whether the array is actually in the sorted order by checking the fundamental rule for the array to be sorted. For all i, a[i] <= a[i + 1], condition should hold.
/* test to ensure that the array is in sorted order */
void test_array_is_in_order(int arr[]) {
int max = 0;
for (int i = 1; i < LENGTH; i ++) {
if (arr[i] >= arr[i - 1]) {
max = arr[i];
} else {
printf("Error. Out of order sequence: %d found\n", arr[i]);
return;
}
}
printf("Array is in sorted order\n");
}Having understood the basic blocks, let me present to you the whole code with comments.
/*
* Parallel Merge Sort
* Created by Malith Jayaweera on 1/11/19.
* Published at malithjayaweera.com for public use.
* Copyright © 2019 Malith Jayaweera. All rights reserved.
*
*
* This program is free software: you can redistribute it and/or modify
* it under the terms of the GNU General Public License as published by
* the Free Software Foundation, either version 3 of the License, or
* (at your option) any later version.
* This program is distributed in the hope that it will be useful,
* but WITHOUT ANY WARRANTY; without even the implied warranty of
* MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the
* GNU General Public License for more details.
* You should have received a copy of the GNU General Public License
* along with this program. If not, see <http://www.gnu.org/licenses/>.
*/
#include <stdio.h>
#include <stdlib.h>
#include <pthread.h>
#include <sys/time.h>
/* define variables for the problem */
#define SEED 100
#define LENGTH 100000
#define UPPER_LIM 10000
#define LOWER_LIM 1
#define NUM_THREADS 2
/* define derived values from the variables */
const int NUMBERS_PER_THREAD = LENGTH / NUM_THREADS;
const int OFFSET = LENGTH % NUM_THREADS;
int arr[LENGTH];
/* function definitions */
int generate_random_number(unsigned int lower_limit, unsigned int upper_limit);
void merge_sort(int arr[], int left, int right);
void merge(int arr[], int left, int middle, int right);
void* thread_merge_sort(void* arg);
void merge_sections_of_array(int arr[], int number, int aggregation);
void test_array_is_in_order(int arr[]);
int main(int argc, const char * argv[]) {
srand(SEED);
struct timeval start, end;
double time_spent;
/* initialize array with random numbers */
for (int i = 0; i < LENGTH; i ++) {
arr[i] = generate_random_number(LOWER_LIM, UPPER_LIM);
}
/* begin timing */
pthread_t threads[NUM_THREADS];
gettimeofday(&start, NULL);
/* create threads */
for (long i = 0; i < NUM_THREADS; i ++) {
int rc = pthread_create(&threads[i], NULL, thread_merge_sort, (void *)i);
if (rc){
printf("ERROR; return code from pthread_create() is %d\n", rc);
exit(-1);
}
}
for(long i = 0; i < NUM_THREADS; i++) {
pthread_join(threads[i], NULL);
}
merge_sections_of_array(arr, NUM_THREADS, 1);
/* end timing */
gettimeofday(&end, NULL);
time_spent = ((double) ((double) (end.tv_usec - start.tv_usec) / 1000000 +
(double) (end.tv_sec - start.tv_sec)));
printf("Time taken for execution: %f seconds\n", time_spent);
/* test to ensure that the array is in sorted order */
/* test_array_is_in_order(arr); */
return 0;
}
/* generate random numbers within the specified limit */
int generate_random_number(unsigned int lower_limit, unsigned int upper_limit) {
return lower_limit + (upper_limit - lower_limit) * ((double)rand() / RAND_MAX);
}
/* merge locally sorted sections */
void merge_sections_of_array(int arr[], int number, int aggregation) {
for(int i = 0; i < number; i = i + 2) {
int left = i * (NUMBERS_PER_THREAD * aggregation);
int right = ((i + 2) * NUMBERS_PER_THREAD * aggregation) - 1;
int middle = left + (NUMBERS_PER_THREAD * aggregation) - 1;
if (right >= LENGTH) {
right = LENGTH - 1;
}
merge(arr, left, middle, right);
}
if (number / 2 >= 1) {
merge_sections_of_array(arr, number / 2, aggregation * 2);
}
}
/** assigns work to each thread to perform merge sort */
void *thread_merge_sort(void* arg)
{
int thread_id = (long)arg;
int left = thread_id * (NUMBERS_PER_THREAD);
int right = (thread_id + 1) * (NUMBERS_PER_THREAD) - 1;
if (thread_id == NUM_THREADS - 1) {
right += OFFSET;
}
int middle = left + (right - left) / 2;
if (left < right) {
merge_sort(arr, left, right);
merge_sort(arr, left + 1, right);
merge(arr, left, middle, right);
}
return NULL;
}
/* test to ensure that the array is in sorted order */
void test_array_is_in_order(int arr[]) {
int max = 0;
for (int i = 1; i < LENGTH; i ++) {
if (arr[i] >= arr[i - 1]) {
max = arr[i];
} else {
printf("Error. Out of order sequence: %d found\n", arr[i]);
return;
}
}
printf("Array is in sorted order\n");
}
/* perform merge sort */
void merge_sort(int arr[], int left, int right) {
if (left < right) {
int middle = left + (right - left) / 2;
merge_sort(arr, left, middle);
merge_sort(arr, middle + 1, right);
merge(arr, left, middle, right);
}
}
/* merge function */
void merge(int arr[], int left, int middle, int right) {
int i = 0;
int j = 0;
int k = 0;
int left_length = middle - left + 1;
int right_length = right - middle;
int left_array[left_length];
int right_array[right_length];
/* copy values to left array */
for (int i = 0; i < left_length; i ++) {
left_array[i] = arr[left + i];
}
/* copy values to right array */
for (int j = 0; j < right_length; j ++) {
right_array[j] = arr[middle + 1 + j];
}
i = 0;
j = 0;
/** chose from right and left arrays and copy */
while (i < left_length && j < right_length) {
if (left_array[i] <= right_array[j]) {
arr[left + k] = left_array[i];
i ++;
} else {
arr[left + k] = right_array[j];
j ++;
}
k ++;
}
/* copy the remaining values to the array */
while (i < left_length) {
arr[left + k] = left_array[i];
k ++;
i ++;
}
while (j < right_length) {
arr[left + k] = right_array[j];
k ++;
j ++;
}
}
Please leave a comment if this post was helpful. 🙏 It’s very much appreciated.
I’ve written a new test suite to verify the validity of the merge sort algorithm. The code is available at: https://malithjayaweera.com/2019/12/why-researchers-should-use-c-unit-testing/
Thanks for the article. I wonder what line “merge_sort(arr, left + 1, right);” in thread_merge_sort procedure suppose to do?
Thank you for the comment. It’s a code refactoring issue. I’ve fixed the problematic lines. No impact on accuracy but it causes a redundant computation.